Forward Problem
dMRI and the Bloch-Torrey equation
Diffusion-weighted MRI (dMRI) is governed by the Bloch-Torrey equation, which is a 2nd order PDE:
\(\frac{\partial \bm{M}}{\partial t} = -i(\gamma \bm{G} \cdot \bm{x})\bm{M} - \frac{\bm{M}}{T_2} - D \nabla^2 \bm{M}\) .
Solving the Bloch-Torrey equation for different microstructural geometries allows us to determine what the dMRI signal should be for that particular microstructure. Unfortunately, dMRI in muscle has a resolution size of 1-2 mm while the microstructure being measured is on the order of 10 microns (0.001 mm). This means that when we measure the dMRI signal, we only measure the voxel average of the dMRI signal.
simplified REV model
This averaging smears the signal, making it difficult to directly connect the dMRI measurement with the underlying microstructure. However, because of muscle’s semi-periodic structure, it is still possible to infer microstructural parameters from the dMRI signal. Muscle consists of many long fibers that are tightly bundled together. By assuming that these fibers all have the same cross-sectional shape and are packed together in the same way, we can approximate the muscle structure using a simplified model that we call a Representative Elementary Volume (REV). This REV model allows us to parameterize the muscle and understand how changes in these microstructural parameters (for example, the cell diameter) lead to changes in the dMRI signal.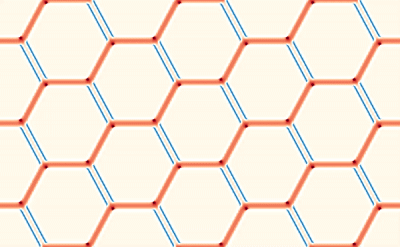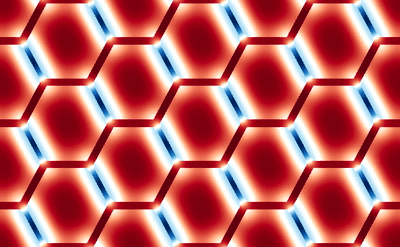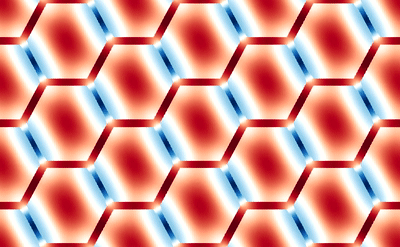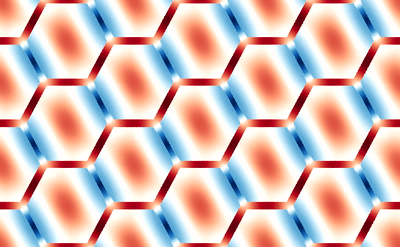
Solving the Bloch-Torrey equation
Solving the Bloch-Torrey equation can be done analytically for simple shapes, however, over more complex domains, such as the REV, it is necessary to use numerical methods. We use the lattice Boltzmann method which is an efficient solution technique that can be easily parallelized to take advantage of high-performance computing (HPC) resources [1]. Thanks to a startup allocation from XSEDE, we have shown that the model can efficiently scale to over 160 cores on SDSC’s Comet cluster.
Validating existing models
With this LBM model, we have an accurate solution of the Bloch-Torrey equation that accurately represents the dMRI physics. This allows us to treat it as an in-silico phantom (a computer-based testing device) that can be used to validate new and existing models of dMRI [2]. The advantage of using an in-silico phantom is exact knowledge of the underlying microstructure, something that is very difficult to measure in real biological tissue. This allows rigorous validation that a model is able to capture the underlying structural behavior and physics of dMRI before applying them to the more complex case of real biological tissue, where noise and difficulty in verifying the underlying tissue complicate the validation process.
Sensitivity analysis
Another advantage of this in-silico phantom is being able to easily change the microstructural parameters to see how these changes affect the dMRI signal. By doing this in a systematic fashion, we can perform a sensitivity analysis to understand how changes in tissue microstructure and dMRI pulse parameters lead to changes in the dMRI signal [3]. Understanding this sensitivity helps us interpret dMRI measurements and design pulse sequences that can efficiently encode microstructural information. Both of these insights are important in giving us the correct cools to accurately solve the inverse problem.
Simulating realistic histology images

from histology image
While the simplified REV model allows us to precisely control and measure changes in the microstructure, skeletal muscle has a more complex, disordered organization. Simulating dMRI over realistic domains obtained from histology images of muscle allows us to compare how our simplified REV compares with more realistic geometries. It also allows us to examine how structural features not considered by the REV might affect the dMRI signal. By performing these histologically informed simulations, we have found that ellipticity of fascicles may explain the observed transverse anisotropy of the measured diffusion tensor [4].
Related Publications
[1] Naughton NM, Tennyson C, and Georgiadis JG. Lattice Boltzmann method for simulation of diffusion magnetic resonance imaging physics in heterogeneous tissue models. Journal of Computational Physics, (under review).
[2] Naughton NM and Georgiadis JG. Comparison of two-compartment exchange and continuum models of dMRI in skeletal muscle. Physics in Medicine and Biology, (in revision).
[3] Naughton, NM and Georgiadis JG. Global Sensitivity Analysis of Skeletal Muscle dMRI: Effects of Microstructural and PGSE Pulse Parameters. Magnetic Resonance in Medicine, (in preparation).
[4] Naughton NM, Wang A, and Georgiadis JG. Fascicle Ellipticity as an Explanation of Transverse Anisotropy in Diffusion MRI Measurements of Skeletal Muscle. ISMRM Annual Meeting (May 2019), Montreal, Canada (poster)