Inverse Problem
Estimating muscle microstructure from dMRI measurements
The inverse problem, as its name implies, is ultimately about working in the inverse direction as the forward problem. We use the dMRI signal that is measured when you get an MRI and from it infer the microstructural properties of your muscle. Going from the dMRI signal to the underlying microstructure is not straight forward. Often, models of the forward problem are used and the possible microstructural parameters are varied until the predicted dMRI signal matches the measured dMRI signal. These microstructure predictions can then be compared with the numerical LBM model to determine if they accurately capture changes in microstructure [2, 5]. This often requires many model evaluations so having a computationally efficient model is important.
Meta-model of Bloch-Torrey equation
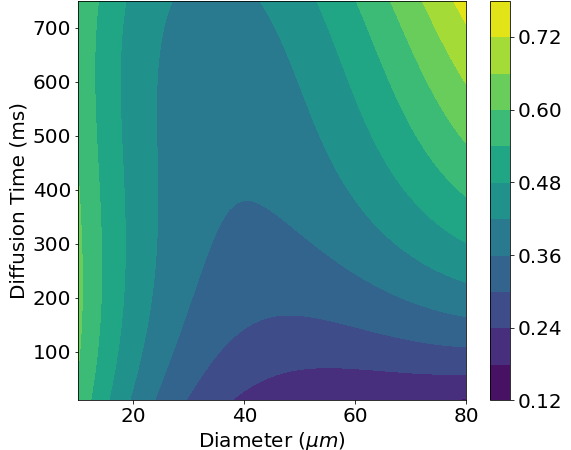
The numerical LBM model of dMRI is computationally expensive. To allow for faster solutions, we can use a meta-model of the LBM model. A meta-model is a model of a model; it models the relationship between the input and the output of the underlying model with no regard for the actual physics [1, 3]. Since we are trying to adjust the microstructural parameters to match the measured dMRI signal, this is perfect for our needs. The meta-model fits a polynomial to previous results from the numerical LBM model. This yields a polynomial expression that is much faster to evaluate than solving the numerical LBM model while still retaining much of the accuracy. One use of this meta-model is being able to easily see how changes in different parameters lead to changes in the measured dMRI signal. For example, we can look at how a change in cell diameter affects fractional anisotropy (FA). Even more interestingly, we can also see how measuring the dMRI at different diffusion times leads to changes in FA. By measuring multiple diffusion times, we can get a ‘fingerprint’ for a specific cell diameter.
PGSE pulse optimization for microstructure encoding
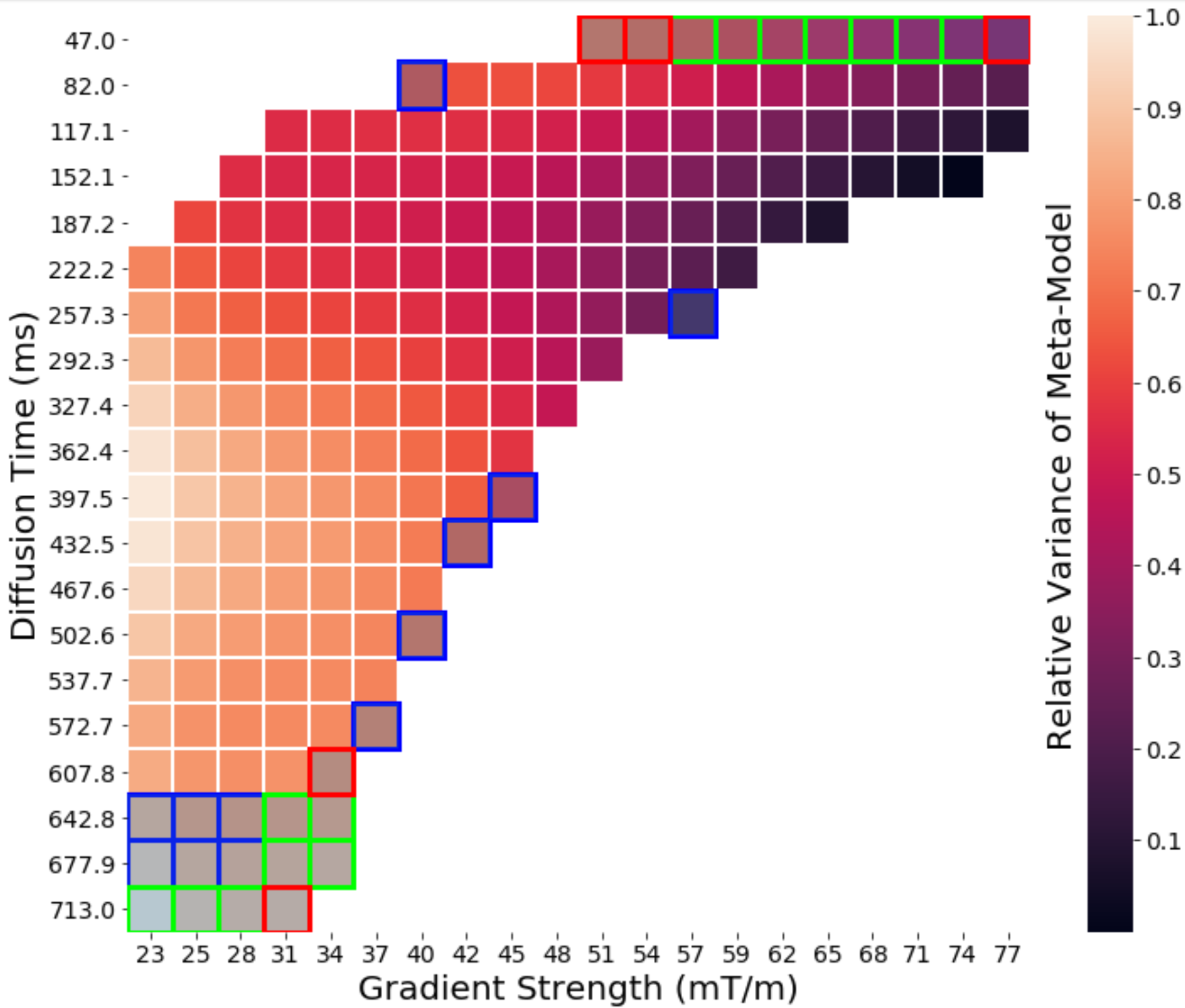
Identifying these fingerprints for different combinations of microstructural parameters helps us estimate microstructure from the dMRI signal, but we also want to know what types of dMRI pulses will best allow us to do this. Being able to acquire the same microstructural information using fewer pulse sequences leads to shorter acquisition times, something anyone who has ever had an MRI can appreciate. Using the meta-model we look at which pulse profiles give the largest range for dMRI measurements, and in particular, what combinations of pulse profiles allows us to encode the most possible information about the microstructure into the dMRI signals [1].
Inverting the numerical LBM model
While the numerical LBM model is slow, it is still the most accurate model available. Because of this, it is a useful test candidate to show that it is possible to recover the microstructure information about the muscle from the dMRI signal. Once this is established, we can work on improving the efficiency of the model. However, even though the LBM model is slow, we can take advantage of the parallelization of the LBM method by using GPU-acceleration. Additionally, by developing fitting methods that allow for parallel model evaluations we can use multiple GPUs to reduce the time it takes to fit the LBM model to the dMRI signal [1].
Machine Learning Models
Does the problem even exist if you don’t use machine learning to try and solve it? Machine learning techniques have shown great promise in being able to solve inverse problems, and this inverse problem is no exception. By generating large training datasets using the numerical model, it is possible to train models to predict the microstructure from the dMRI signal [4]. The disadvantage of these models is they are often not based on the underlying physics of the problem, so they cannot give insight into what is going on. Because of this, it is important to first understand the relationship between microstructure and dMRI, which we do by studying the forward problem. This allows us to know the limits and caveats of the predictions of the machine learning models.
Solving the inverse problem and being able to predict the microstructure of skeletal muscle from dMRI signal will require a combination of different models, each with its own strengths and weakness. By combining these models, we will be able to take a dMRI measurement and estimate the underlying tissue microstructure from it. These microstructural estimates can then be used in micro-mechanical models of muscle. The models help us solve the mechanical problem of understanding how microstructural variations change effective mechanical properties of muscle, and by extension, the ability of the muscle to transmit force and properly function.
Related Publications
[1] Naughton NM and Georgiadis JG. Connecting Diffusion MRI to Skeletal Muscle Microstructure: Leveraging Meta-Models and GPU-acceleration. PEARC19 (July 2019), Chicago, Illinois (platform presentation)
[2] Naughton NM, Gallo NR, Anderson AT, and Georgiadis JG. Comparison of dMRI Models for Skeletal Muscle Microstructure Estimations with Numerical Simulations and Myocardial Porcine Phantom. ISMRM Annual Meeting (May 2019), Montreal, Canada (poster)
[3] Naughton NM, Jain A, and Georgiadis JG. Polynomial Meta-Model of Bloch-Torrey Equation for Track-based Regularization of Microstructural Inversion. ISMRM Annual Meeting (May 2019), Montreal, Canada (poster)
[4] Naughton NM, Gallo NR, Anderson AT, and Georgiadis JG. Microstructural Parameter Estimation of Skeletal Muscle using Random Forest Model of dMRI. ISMRM Annual Meeting (May 2019), Montreal, Canada (poster)
[5] Naughton NM, Gallo NR, Vaicik M, Anderson AT, Sutton BP, and Georgiadis JG. Estimation of Extracellular Matrix Diffusion Properties in Decellularized Porcine Myocardium from DTI. ISMRM Annual Meeting (June 2018), Paris, France (poster)